- Si è
osservato che dalla Legge di Gravitazione Universale
dell’intramontabile Newton si deduce che, a differenza di quanto
asserito da Galileo, le modalità di caduta dei gravi sulla
superficie terrestre dipendono dalla massa del corpo che cade. Infatti
mentre per Galileo i gravi subiscono solo passivamente l’azione
gravitazionale della Terra, con Newton, che estende a tutti i corpi del
cosmo un proprio potere gravitazionale, i gravi, attivamente e per
proprio conto, attraggono, ed in proporzione della loro massa, la Terra
verso se stessi e quindi il tempo di caduta di un corpo sulla
superficie terrestre è anche funzione della massa che cade.
Infatti dalla soluzione del Problema dei due Corpi di Newton (e quindi
dalla Meccanica Celeste classica attuale) si ricava facilmente [1,2,3]
che l’accelerazione di un grave è data dalla formula
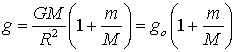 ,
,
dove m, M ed R sono rispettivamente le masse del grave, della Terra ed il raggio terrestre. Dalla detta formula si ha quindi che solo quando il rapporto m/M è completamente trascurabile si ottiene, come caso limite, la legge di caduta di Galileo. Sulla superficie terrestre il rapporto m/M, per un grave di ben una tonnellata, è dell’ordine di 1x10-22, sicché le differenze di accelerazione tra i vari gravi sfuggono ancora a qualsiasi controllo sperimentale, anche se eseguito con i più raffinati strumenti moderni.
- Se dunque, allo stato
attuale, è ancora impossibile verificare quanto previsto
dall’attuale Meccanica Celeste classica sulla superficie
terrestre, ben diversamente stanno le cose nel nostro sistema solare.
In tal caso il detto rapporto va da 1.65x10-7 ([1]), per la coppia
Sole-Mercurio, a 9.54x10-4, nel caso del sistema binario Sole-Giove
([2]). Ciò comporta che il moto impresso al Sole dalla massa del
generico pianeta non è affatto trascurabile, mentre, per contro,
nelle attuali teorie delle perturbazioni planetarie, sia nel problema
dei due che in quello degli enne Corpi, il Sole viene sempre
considerato assolutamente fisso rispetto alle stelle fisse. Tanto
è vero che il moto relativo misurato tra il punto γ ed il
Sole, ammontante a ben 50” d’arco sessagesimale
all’anno, viene ancora oggi interamente attribuito al solo moto
proprio del detto punto γ, giustificandolo (o tentando di
giustificarlo) tutto con il solo fenomeno della precessione lunisolare
e pensando invece il Sole assolutamente fisso, nonostante le non
trascurabili azioni di scalzamento o di rinculo che esso subisce dai
vari pianeti ed in particolare da Giove. In conclusione dimostreremo
che la mancata previsione da parte della Meccanica Celeste
dell’avanzamento del perielio di Mercurio è esclusivamente
dovuta al fatto, squisitamente teorico, che detta teoria, in alcuni
precisi momenti dello sviluppo dell’algoritmo di calcolo che
individueremo, inconsciamente presuppone, contrariamente ai suoi
presupposti originari, l’assoluta fissità del Sole.
Ma questa presupposta gratuita fissità del Sole che, nel caso specifico di Mercurio, costa alla M.C. un errore di previsione di appena 44’’ al secolo, la scuote e la sconvolge fortemente nella spiegazione del grandioso fenomeno della precessione lunisolare, spiegazione nella quale, ancora una volta, essa tenta di attribuire ai soli fenomeni giroscopici il moto relativo di ben 50’’ all’anno registrati tra il Sole ed il punto γ, al solo moto di quest’ultimo, spiegazione, per altri aspetti non sospetti, fortemente contestata già a suo tempo da scienziati del livello di Bernoulli, Eulero e d’Alambert, addirittura nel ‘700. Secondo i citati Autori, la spiegazione di Newton non riuscirebbe da sola a giustificare l’intero fenomeno osservato, ma questi studiosi ed illustri scienziati non avanzarono altre ipotesi o effetti che avrebbero potuto colmare questa deficienza che, secondo gli stessi, spiegherebbe solo circa 30’’ all’anno e non al secolo. Per giunta, le attuali conoscenze circa il geoide terrestre, costituito da una sottile crosta che galleggia su un magma incandescente, pone anche in forte discussione il valore dei momenti d’inerzia del geoide stesso, ovviamente attribuito ad hoc [2], per cui la spiegazione di Newton scenderebbe a qualche decina di secondi all’anno [2]. A questa grossa ed incolmabile deficienza della giustificazione di Newton, come è dimostrato in questa sede, può sopperire appunto lo scalzamento che invece il Sole subisce da tutti i vari pianeti, spostamento indebitamente annullato dalla Meccanica Celeste. Si trova finalmente così la legge con la quale dovrebbe variare lo spostamento del Sole verso il punto γ e si riesce anche a valutare teoricamente la variazione annua che subisce quella che comunemente chiamiamo oggi precessione lunisolare. La figura che segue da l’andamento di questo fenomeno (Fig. 30)
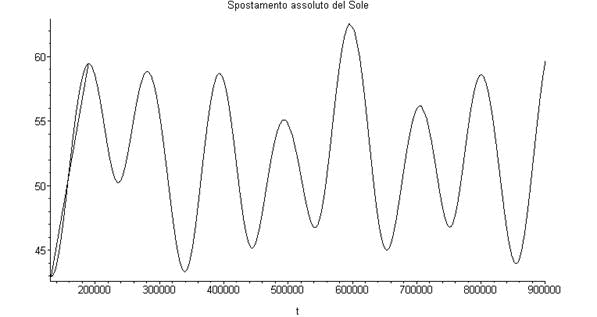
Fig. 30
Sull’ascissa è rappresentato il tempo in anni e sulle ordinate il valore dello spostamento del Sole verso il punto γ dovuto al contributo di tutti i pianeti, inclusi i trascurabili 44’’ al secolo, dovuti all’azione di rinculo del Sole causati dal pianeta Mercurio. La variazione teorica ammonta a ±0.00027 secondi d’arco sessagesimale all’anno. Quella sperimentale, secondo Newcomb, agli inizi del secolo scorso, ammontava a 0.000222. Invece questa variazione è del tutto incomprensibile ed ingiustificabile con l’attuale interpretazione, assolutamente giroscopica.
Si ha quindi l’impressione, per non dire la certezza, che se si rimuove dalla teoria delle perturbazioni della M.C. l’insostenibile ed inopportuna teorica fissità del Sole, che comporta anche dei sostanziali ripensamenti sul tempo siderale, la teoria dell’Insuperabile inglese darà ancora insospettabili, positive e forti sorprese.
[1] Nel prosieguo, si tenga a mente questo numero.
[2] Per il sistema Terra-Luna esso sale addirittura m/M=1.23x10-2
